Trigonometria

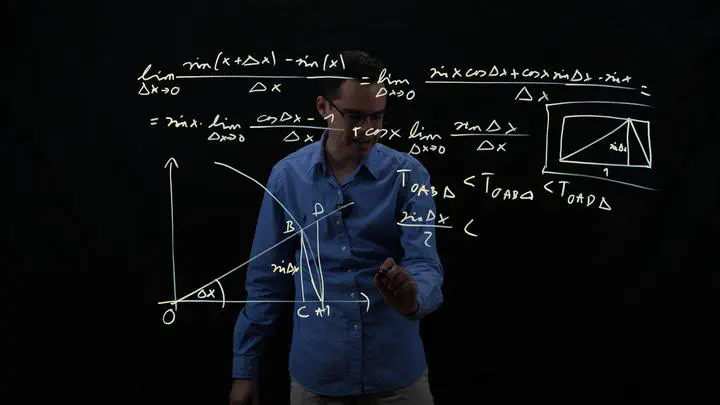
A szögfüggvényeket (és egyáltalán, a trigonometriát) úgy szokás bevezetni, mint a háromszög különböző oldalaival és szögeivel kapcsolatos összefüggéseket. Most nekünk célszerűbb lesz egy másik - ezzel természetesen teljesen egyenértékű - megközelítés, melyben a szögfüggvényeket úgy értelmezzük, mint egy derékszögű koordináta-rendszerben a vízszintes tengellyel adott szöget bezáró, egységnyi hosszú szakasz vízszintes és függőleges vetületeit (amik természetszerűleg a bezárt szög függvényei). Ehhez elsőként azt kell definiálni, hogy egyáltalán mit értünk szög alatt; utána röviden beszélünk a szögek méréséről is. Ez alapján már megadhatjuk a szögfüggvények pontos definícióját. Ezen függvények jelentőségét nehéz lenne túlbecsülni: gyakorlatilag minden matematikát alkalmazó területen megjelennek. Ennek megfelelően részletesebben beszélünk a legfontosabb tulajdonságaikról, külön kitérve a nevezetes azonosságokon túl a szögfüggvények súlyozott összegére, melyek jelentősége különösen nagy egy sor alkalmazásban. Beszélünk a szögfüggvények deriválásáról és sorfejtéséről; ezen ismeretek lehetővé teszik egy nevezetes, gyakran használt közelítés bevezetését, mely kis szögekre működik jól. Végül, bár technikai kérdésnek tűnhet, beszélünk arról is, hogy a gyakorlatban hogyan lehet, illetve hogyan célszerű a szögfüggvények kiszámítása bizonyos konkrét értékre vagy értékekre.